Co-varying predictors can be a messy business. They make estimates unstable, reducing our statistical power and making interpretation more difficult. In this post I will demonstrate how ignoring the presence of co-variation between predictors when exploring our models can lead to odd results and how we might deal with this issue.
Our Model
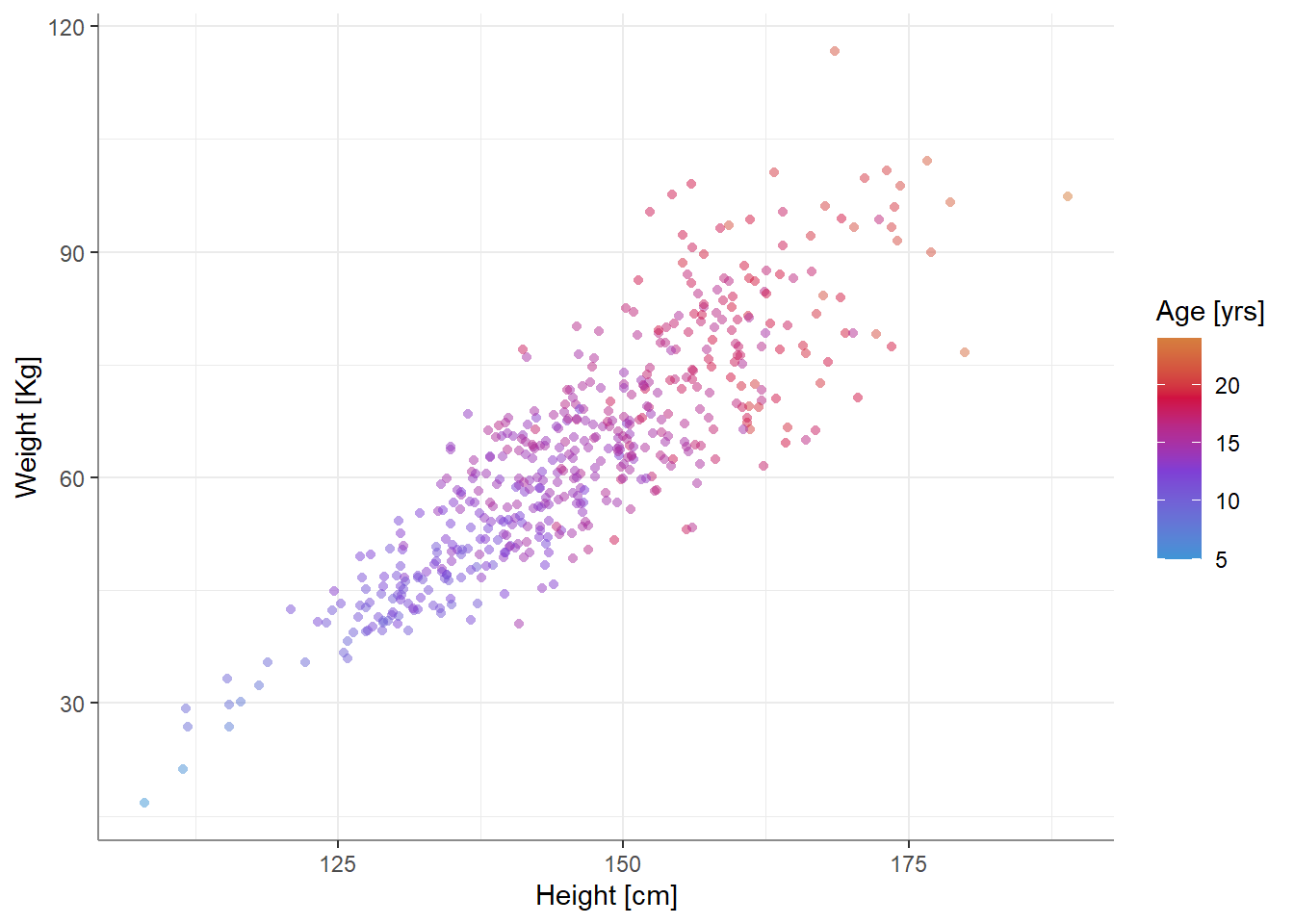
For our example, we will use some (fake) developmental-growth data - we have the height and weight of 500 individuals between the ages of 5 and 24. We can plot our tri-variate data like so:
This generally looks as one might expect - taller people weigh more, older people are taller and weigh more as well.
Predicting Weight from Height
Let us fit an OLS linear model1 to predict weight from height and age:
fit <- lm(weight ~ height + age, data = data)
summary(fit)#>
#> Call:
#> lm(formula = weight ~ height + age, data = data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -23.8960 -3.9637 -0.0438 4.3013 25.8607
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -51.97123 5.27409 -9.854 <2e-16 ***
#> height 0.53458 0.05741 9.312 <2e-16 ***
#> age 2.47319 0.25311 9.771 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 7.009 on 497 degrees of freedom
#> Multiple R-squared: 0.7856, Adjusted R-squared: 0.7847
#> F-statistic: 910.4 on 2 and 497 DF, p-value: < 2.2e-16Unsurprisingly, both age and height are positively related to weight.
Let’s explore our model - specifically, we want to see what weight can we expect for 3 individuals of the following heights: 120, 145, and 170cm. We can do this with emmeans:
library(emmeans)
em_by_height <- emmeans(fit, ~ height, at = list(height = c(120, 145, 170)))
em_by_height#> height emmean SE df lower.CL upper.CL
#> 120 49.0 1.536 497 46.0 52.0
#> 145 62.4 0.321 497 61.7 63.0
#> 170 75.7 1.402 497 73.0 78.5
#>
#> Confidence level used: 0.95We can also add these expected values to the plot from above:
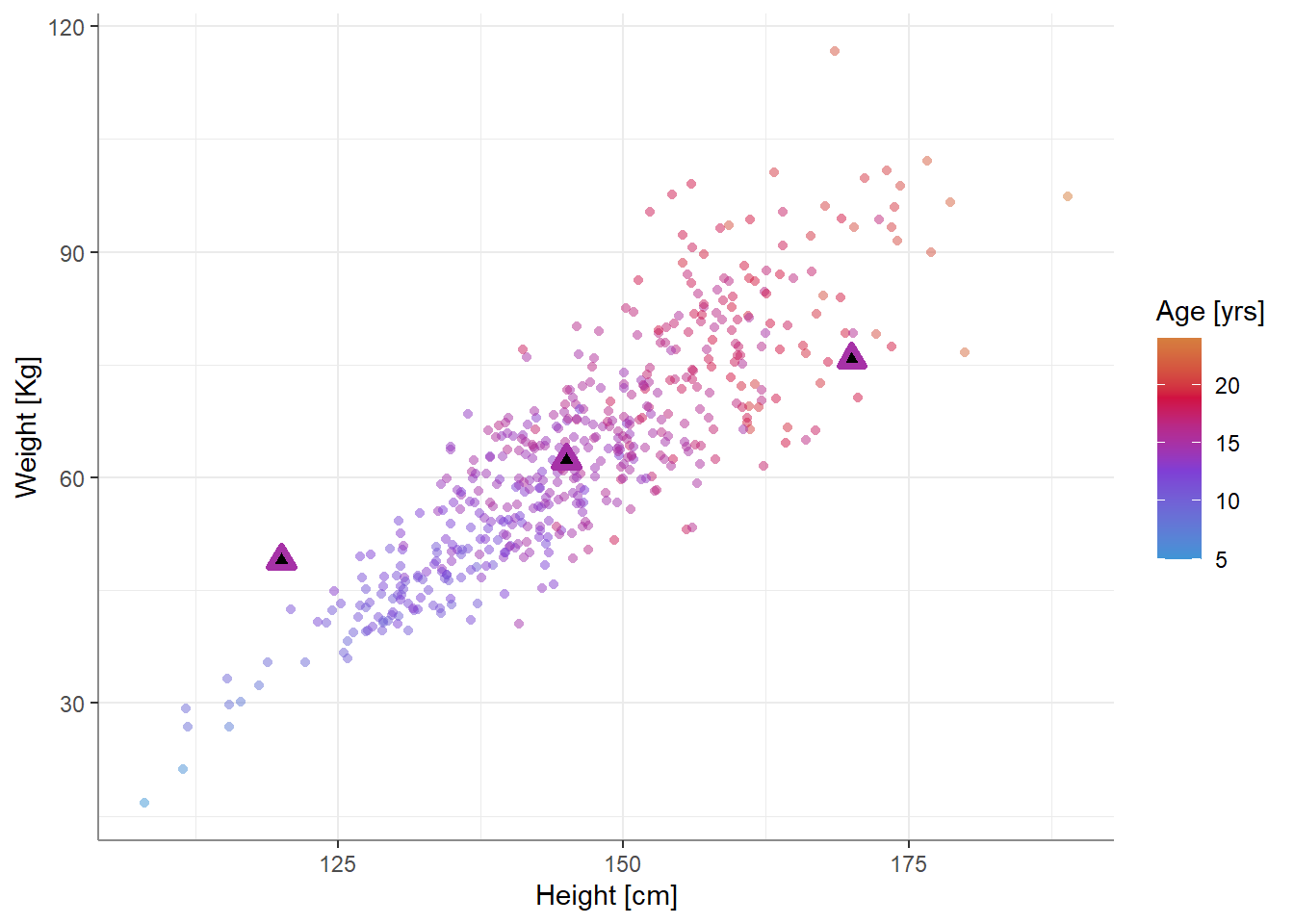
Something seems off - the expected value for a person 120cm tall seems too high, while the expected value for a person 170cm tall seems too low. Why is that? What’s going on?
First, let’s talk about the elephant in the room - there is obvious multicollinearity between our predictors! If we’re not sure, we can use performance::check_collinearity() to validate this:
performance::check_collinearity(fit)#> # Check for Multicollinearity
#>
#> Moderate Correlation
#>
#> Term VIF VIF 95% CI Increased SE Tolerance Tolerance 95% CI
#> height 5.26 [4.51, 6.17] 2.29 0.19 [0.16, 0.22]
#> age 5.26 [4.51, 6.17] 2.29 0.19 [0.16, 0.22]But how is this related to the funky estimates we got?
Well, this has to do with what we do with the other predictors when exploring a single predictor. In our case, what happens to age when we’re exploring the role of height in our model?
The common and almost default approach is to fix age to a constant. This is really what our model does in the first place: the coefficient of height represents the expected change in weight while age is fixed and not allowed to vary. What constant? A natural candidate (and indeed emmeans’ default) is the mean. In our case, the mean age is 14.9 years. So the expected values produced above are for three 14.9 year olds with different heights. But is this data plausible? If I told you I saw a person who was 120cm tall, would you also assume they were 14.9 years old?
No, you would not. And that is exactly what covariance and multicollinearity mean - that some combinations of predictors are more likely than others.
Predicting Weight from Height (accounting for covariance among predictors)
So how do we get more reasonable expected weights?
Well, we can allow age to vary in our prediction. Vary how? Well, vary with height! So instead of asking “what are the expected heights of 3 individuals that are 120, 145, and 170cm tall, all of the same age”, we can ask “what are the expected heights of 3 individuals that are 120, 145, and 170cm tall, of height-appropriate ages”.
In emmeans this can be done by specifying a predictive formula in cov.reduce. For example:
(rg_multicov <- ref_grid(fit,
at = list(height = c(120, 145, 170)),
cov.reduce = list(age ~ height))) # This!#> 'emmGrid' object with variables:
#> height = 120, 145, 170
#> age = (predicted by other variables)rg_multicov@grid#> height age .wgt.
#> 1 120 9.537649 1
#> 2 145 14.640867 1
#> 3 170 19.744085 1emmeans(rg_multicov, ~ height)#> height emmean SE df lower.CL upper.CL
#> 120 35.8 0.727 497 34.3 37.2
#> 145 61.8 0.315 497 61.1 62.4
#> 170 87.7 0.673 497 86.4 89.1
#>
#> Confidence level used: 0.95We can see from the reference grid (rg_multicov@grid) that age is not fixed, but varies with height.
We can also achieve the same this in a single call to emmeans():
em_by_height2 <- emmeans(fit, ~ height,
at = list(height = c(120,145,170)),
cov.red = list(age ~ height))
em_by_height2#> height emmean SE df lower.CL upper.CL
#> 120 35.8 0.727 497 34.3 37.2
#> 145 61.8 0.315 497 61.1 62.4
#> 170 87.7 0.673 497 86.4 89.1
#>
#> Confidence level used: 0.95What we’ve done is essentially re-introducing multicollinearity into our estimates by allowing age to co-vary with height: each expected value is no longer just a function of height, but it is also a function of the expected age for that height2.
If we plot these estimates, we get…
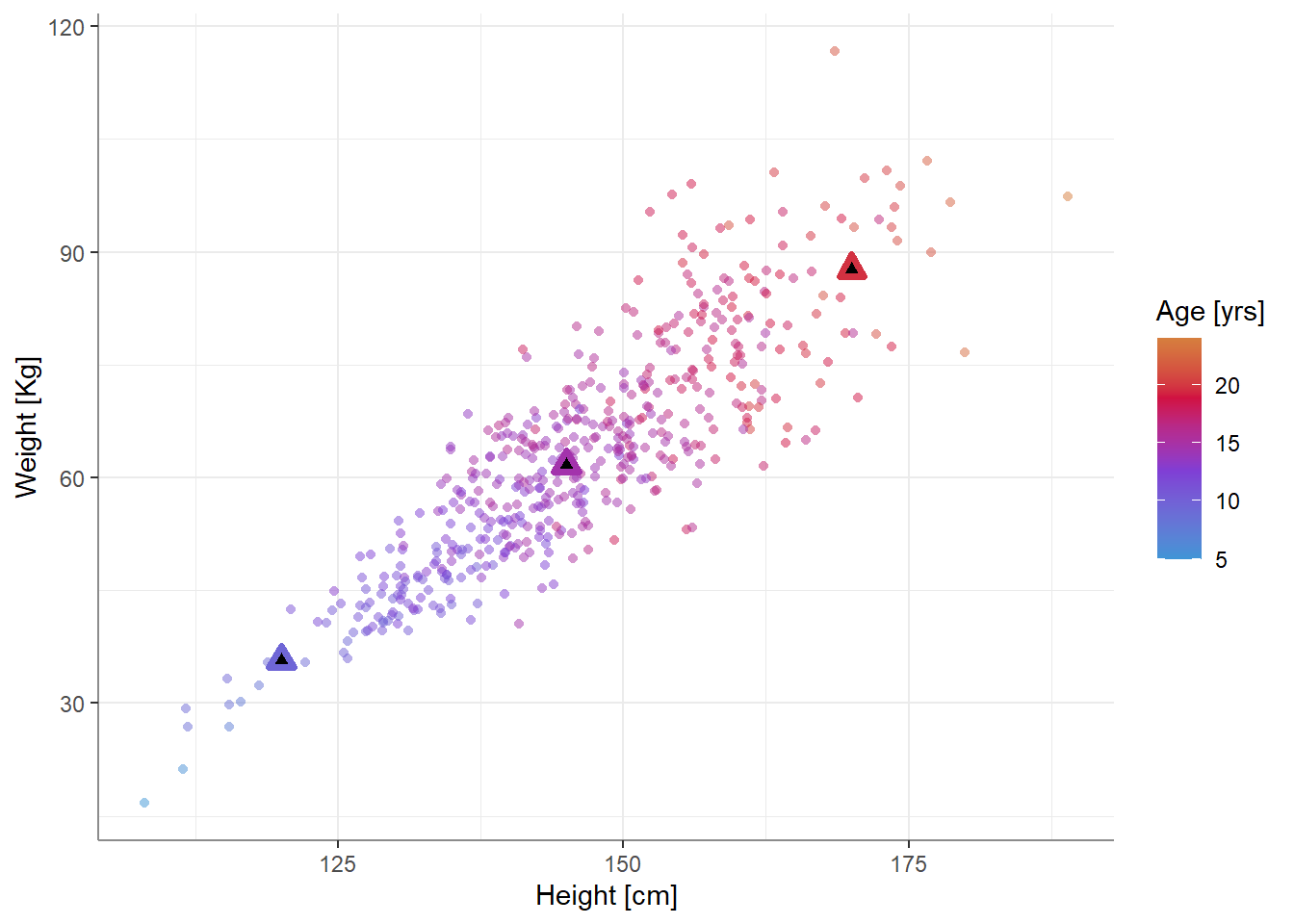
…which seems more reasonable.
Summary
Should you do this whenever you have multicollinearity in your data?
No - not always and not only!
You might want to do this whenever exploring one predictor while fixing other to a constant produces uncommon and unlikely combinations of predictors. In fact, such a situation may arise even when measures of multicollinearity (such as the VIF) are not “too” high, as these usually only measure co-linearity, but other patterns of co-variation my be present in your data. In fact this may be useful in any instance of co-variation among predictors, such as suppression / confounding / mediation (take your pick).3
Note also that producing predictions in this manner does not actually “solve” any of the difficulties of interpretations or any of the oddities that arise in statistical suppression / confounding / mediation. (Extra) care should be taken when interpreting the parameters and the predictions of models with co-varying predictors. In this our case, the question of “does weight vary more with age, or with height” can’t cleanly be answered - what is the meaning of looking at the coefficient (or standardized coefficient) of one predictor while holding the other constant when we know they strongly co-vary?
Just the code please:
knitr::opts_chunk$set(echo = FALSE,
message = FALSE,
comment = "#>")
library(emmeans)
library(ggplot2)
source('../msbblog_theme_pallets.R')
theme_set(theme_msbblog())
library(dplyr)
library(datawizard)
S <- diag(1,3,3)
S[1,2] <- S[2,1] <- 0.9 # add multicollinearity
set.seed(3)
data <- MASS::mvrnorm(500, rep(0,3), S, empirical = TRUE) %>%
data.frame() %>%
rename(height = X1,
age = X2,
e = X3) %>%
mutate(age = change_scale(age, to = c(5, 24)),
height = change_scale(height, to = c(108, 189)),
weight = 7 * (scale(height) + scale(age) + scale(age ^ 2 * e)) + 63)
base_plot <- ggplot(data, aes(height, weight, color = age)) +
geom_point(shape = 16, alpha = 0.5) +
scale_color_gradientn("Age [yrs]",
colours = msbblog_colors[c("blue", "purple", "red", "orange")],
values = c(0, 0.6, 1)) +
labs(y = "Weight [Kg]",
x = "Height [cm]")
base_plot
fit <- lm(weight ~ height + age, data = data)
summary(fit)
library(emmeans)
em_by_height <- emmeans(fit, ~ height, at = list(height = c(120, 145, 170)))
em_by_height
p_dat <- summary(em_by_height)
p_dat$age <- em_by_height@linfct[,"age"]
base_plot +
geom_point(data = p_dat,
aes(y = emmean, color = age),
shape = 24, size = 2, stroke = 2, fill = "black")
performance::check_collinearity(fit)
(rg_multicov <- ref_grid(fit,
at = list(height = c(120, 145, 170)),
cov.reduce = list(age ~ height))) # This!
rg_multicov@grid
emmeans(rg_multicov, ~ height)
em_by_height2 <- emmeans(fit, ~ height,
at = list(height = c(120,145,170)),
cov.red = list(age ~ height))
em_by_height2
p_dat <- summary(em_by_height2)
p_dat$age <- em_by_height2@linfct[,"age"]
base_plot +
geom_point(data = p_dat,
aes(y = emmean, color = age),
shape = 24, size = 2, stroke = 2, fill = "black")