options(contrasts = c('contr.sum', 'contr.poly')) # set effects coding (just once)
fit <- aov(candy_kg ~ decor + decor:costume, data = spooky_data)This spooky post was written in collaboration with Yoav Kessler (@yoav_kessler) and Naama Yavor (@namivor)..
Experimental psychology is moving away from repeated-measures-ANOVAs, and towards linear mixed models (LMM1). LMMs have many advantages over rmANOVA, including (but not limited to):
- Analysis of single trial data (as opposed to aggregated means per condition).
- Specifying more than one random factor (typically crossed random intercepts of subject and item).
- The use of continuous variables as predictors.
Making you look like you know what you’re doing.
Defeating the un-dead / reviewer 2.
- The ability to specify custom models.2
This post will focus on this last point. Specifically, why you should always include main-effects when modeling interactions, and what happens if you don’t (spooky).
Fitting the Right (yet oh so wrong) Model
Say you’ve finally won that grant you submitted to study candy consumption during ghostly themed holidays. As part of your first study, you decide to measure the effects of costume type (scary / cute) and level of neighborhood decor (high / low levels of house decorations) on the total weight of collected candy (in Kg). A simple, yet informative 2-by-2 design.
Being the serious scientist you are, you have several hypotheses:
- A main effect for decor level - neighborhoods with more decorations will overall give out more candy.
- No main effect for costume - overall, children with cute and scary costumes will receive the same amount of candy (in Kg).
- A decor level \(\times\) costume interaction - high decor neighborhoods will favor scary costumes, while low decor neighborhoods will favor cute costumes.
It would only make sense to specify your statistical model accordingly - after all, why shouldn’t your model represent your hypotheses?
In R, such a model is described as candy_kg ~ decor + decor:costume, instructing R to model candy_kg as a function of the effect for decor + the interaction decor:costume.
And so, you fit the model:
| Term | df | SS | MS | F | p-value | \(\eta^2\) | |
|---|---|---|---|---|---|---|---|
| decor | decor | 1 | 30.00 | 30.00 | 23.64 | <0.001 | 0.10 |
| decor:costume | decor:costume | 2 | 120.00 | 60.00 | 47.28 | <0.001 | 0.40 |
| Residuals | Residuals | 116 | 147.20 | 1.27 |
As predicted, you find both a significant main effect for decor and the interaction decor \(\times\) costume, with the interaction explaining 40% of the variance in collected candy weight. So far so good - your results reflect your hypotheses!
But then you plot your data, and to your horror you find…
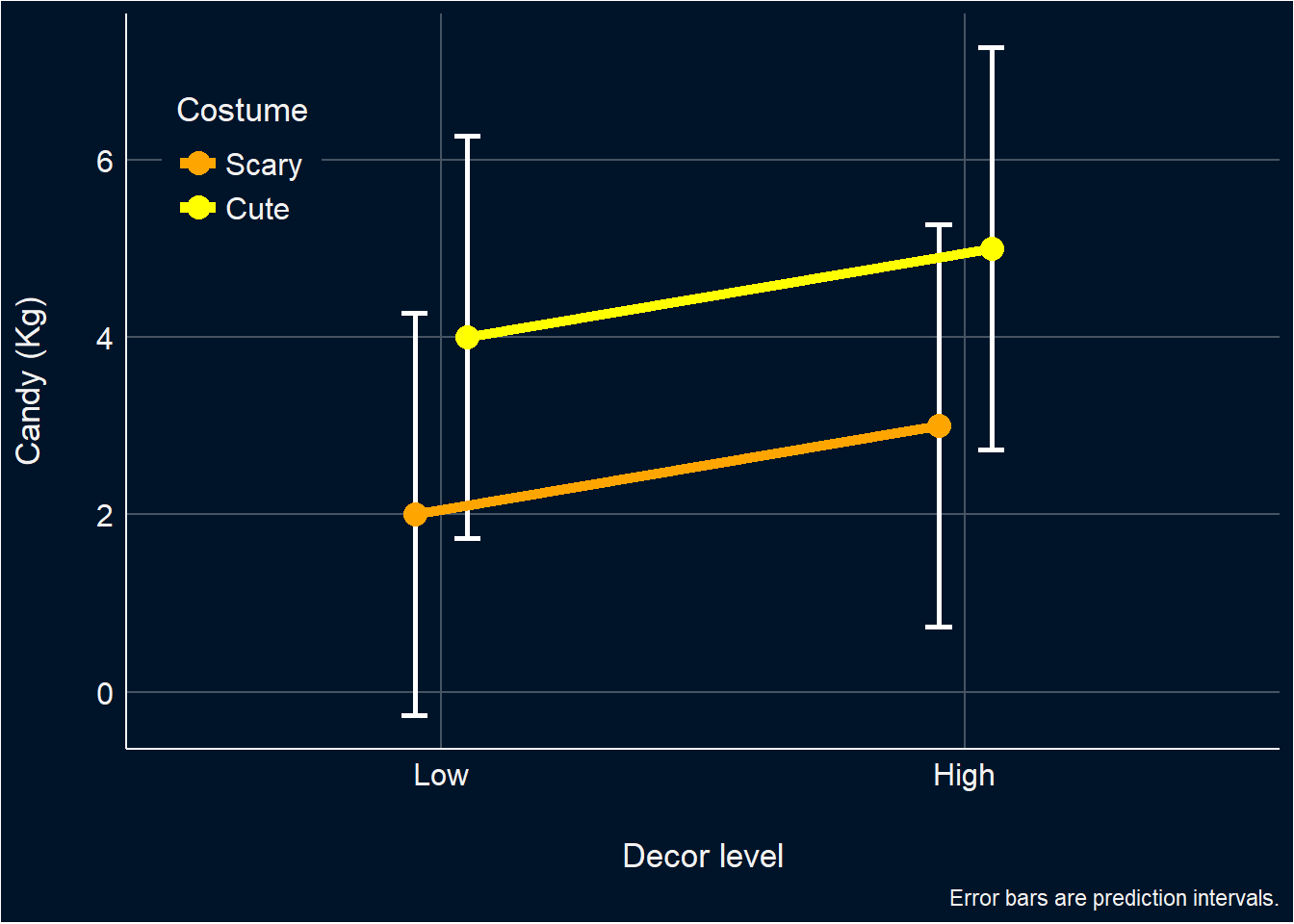
It looks like there is no interaction at all! Your interaction was nothing more than a ghost! An apparition! How is this possible?? Where has all of variance explained by it gone???

In fact, had you fit the full model, you would have found:
fit <- aov(candy_kg ~ decor * costume, data = spooky_data)| Term | df | SS | MS | F | p-value | \(\eta^2\) | |
|---|---|---|---|---|---|---|---|
| decor | decor | 1 | 30.00 | 30.00 | 23.64 | <0.001 | 0.10 |
| costume | costume | 1 | 120.00 | 120.00 | 94.56 | <0.001 | 0.40 |
| decor:costume | decor:costume | 1 | 0.00 | 0.00 | 0.00 | >0.999 | 0.00 |
| Residuals | Residuals | 116 | 147.20 | 1.27 |
The interaction actually explains 0% of the variance! And the effect of costume is the one that explains 40% of the variance!3 How could this be?? Have we angered Fisher’s spirit somehow?
What happened was that because we did not account for costume in our model, the variance explained by costume was swallowed by the interaction decor \(\times\) costume!
The Math
If you find math too scary, feel free to skip to conclusion.
Travel back to Intro to Stats, and recall that the interaction’s sum-of-squares - \(SS_{A\times B}\) - is calculated as:
This is a simplification of the following equation:
Where \((\bar{x}_{i.} - \bar{\bar{x}}_{..})\) represents the main effect for \(A\) and \((\bar{x}_{.j} - \bar{\bar{x}}_{..})\) represents the main effect for \(B\). We can see that \(SS_{A\times B}\) represents the deviation from the additive model - i.e., it is the degree by which the observed cells’ means deviate from what would be expected if there were only the two main effects.
When we exclude the main effect of \(B\) from out model, we are telling our model that there is no need to estimate the main effect. That is, we set \((\bar{x}_{.j} - \bar{\bar{x}}_{..})=0\). The resulting \(SS_{A\times B}\) is computed not as above, but as:
This formula represents the degree by which the observed cells’ means deviate from what would be expected if there was only the main effect of \(A\). But now if the cells’ means deviate in a way that would otherwise have been part of a main effect for \(B\), the cells’ deviations from the main effect for \(A\) will now include the deviations that would otherwise have been accounted for by a main effect of \(B\)! This results in the main effect for \(B\) essentially getting “pooled” into \(SS_{A\times B}\). Furthermore, had you also excluded a main effect for \(A\), this effect too would have been “pooled” into the so-called \(A\times B\) interaction.
In other words:
When we don’t estimate (model) main effects, we change the meaning of interactions - they no longer represents a deviation from the additive model.
Conclusion
Sure, you can specify a model with no main effect and only interactions, but in such a case the interactions no longer mean what we expect them to mean. If we want interactions to represent deviation from the additive model, our model must also include the additive model!
For simplicity’s sake, this example has focused on a simple 2-by-2 between subject design, but the conclusions drawn here are relevant for any design in which a factor interacts with or moderates the effect of another factor or continuous variable.
code for data generation
library(tidyverse)
M <- c(1,2,3,4) + 1 # 4 means with no interaction
n <- 30
e <- scale(rnorm(n),center = TRUE, scale = FALSE) # some error
spooky_data <- expand.grid(decor = c("Low","High"),
costume = c("Scary","Cute")) %>%
mutate(candy_kg = map(M, ~ .x + e)) %>%
unnest(cols = candy_kg)